بقلم نضال شمعون
باحث في المعهد العالي
الحوسبة الكمومية
Quantum Computation
أولاً) مقدّمة تاريخية
الحاسوب الكمومي آلةٌ تمكِّن من استعمال الظواهر الكمومية من أجل تخزين المعلومات وإنجاز الحسابات.
في عام 1982 اقترح فاينمان [Feynman 1982] مفهومَ محاكاة الفيزياء بواسطة الحاسوب الكمومي، فبيّن إمكان تطوير نوع جديدٍ من الحواسيب لا يمكن توصيفُه بواسطة آلات تورينغ، يعتمد على الخواصّ الكمومية للجسيمات، والاستفادة من الحسابات المعقّدة التي تُجريها الطبيعة ضمنيًّا في الحسابات الكمومية بغرض تصميم حاسوب ذي قوة حاسوبية كبيرة.
وفي عام 1985 طوَّر دويتش Deutsch نظرية الحوسبة الكمومية، وبيّن بمثالٍ مُبسَّط قدرة الحاسوب الكمومي على القيام بعمليات التحليل بسرعة أكبر من سرعة أيّ خوارزمية تقليدية [Deutsch 1985].
وفي عام 1996 جرى تطوير خوارزميّات كمومية لعمليّات البحث (غوفر [Gover 1996]) والتحليل إلى عوامل أولية (شور Shor 1997 [Shor 1997]) مع تطبيقاتٍ في التعمية والأمان، وبدأت البحوث العلمية المتعلقة بكيفية بناء حواسيب كمومية.
ومنذ عهد قريب وفَّرت IBM للعموم حاسبًا كموميًّا قابلًا للبرمجة [IBM quantum experience].
ثانيًا) البِتّ الكمومي (أو الكيوبِتّ) Qubit
تسمَّى واحدةُ المعلومات في الحوسبة التقليدية البِتّ bit، وتكون إحدى حالتَين states (0 أو 1) في أي لحظة زمنية. أمَّا واحدةُ المعلومات في الحوسبة الكمومية فتسمَّى الكيوبت (أو البت الكمومي)، وتكون - عند إجراء عملية القياس measurement عليها - في إحدى هاتين الحالتين، ويمكن أن تكون قبل إجراء عملية القياس في حالةِ تركيب خطّيّ linear superposition (أو تراكب) من الحالتين 0 و1 (أي كما لو كان للكيوبت القيمتان 0 و 1 معًا!).
عند إجراء القياس، يكون للكيوبت قيمة واحدة من القيمتين 0 و 1، ونقول إن الكيوبت تداعى (أو انهار) collapse نحو إحدى هاتين القيمتين، ويكون احتمال تداعيه نحو إحدى القيم متناسبًا مع مربَّع العامِل الموافِق في التركيب الخطّي.
نستعمل عادةً مصطلح الكيت ket للكيوبت، حيث يمثل الكيت بساي |ψ⟩ في حالة كيوبت وحيد شعاعَ واحدة في فضاء هلبرت عقدي ذي بعدين:  ، وحيث تمثل
، وحيث تمثل  حالتَي القياس أو الحالتَين الصِّرفتَين pure التي يمكن للكيوبت التداعي نحوهما بقيمتين احتماليتين |a0|2, |a1|2 على الترتيب[1].
حالتَي القياس أو الحالتَين الصِّرفتَين pure التي يمكن للكيوبت التداعي نحوهما بقيمتين احتماليتين |a0|2, |a1|2 على الترتيب[1].
يمكن ترميز الكيوبت إذن بالمساواة:

حيث يحقق الوسيطان (θ زاوية الكيت) و (ϕ طور الكيت) العلاقة 0 ≤ θ ≤ π , 0 ≤ ϕ ≤ 2 π، ومن ثَم يمكن تمثيل الكيوبت بنقطةٍ على الكرة الواحدية الثنائية البعد S2 ذات الإحداثيّات كروية (r = 1, θ, ϕ) المسماة كرة بلوخ Bloch Sphere، كما في الرسم المُوضَّح في الشكل (1).

الشكل (1): كرة بلوخ، وتمثيل الكيوبت عليها.
ثالثًا) البوّابات الوحيدة الكيوبت Single-qubit Gates
هي مؤثّرات خطية تنقل الكيوبت إلى كيوبت آخر. ولما كانت طويلة الكيوبت تساوي الواحد دومًا وجب أن تكون هذه المؤثّرات واحدية unitary، ومن ثَم يمكن النظر إلى البوّابات على أنها دورانات على كرة بلوخ.
فإذا عرّفنا بوابة-إكس بـ  نجد:
نجد:
 ، و X |1⟩ = |0⟩ ،
، و X |1⟩ = |0⟩ ،
ومن ثَم تنقل البوابةُ الكيتَ |x ⟩ إلى |x ⊕ 1⟩، حيث يدل الرمز ⊕ على الجمع بالمقاس 2. ومن ثَم فإن البوابة X تمثل عملية النفي NOT التقليدية التي تقلب الـ 0 إلى 1 وبالعكس. وعمومًا تقلب البوابة معامِلَي الكيوبت أحدهما إلى الآخر:  .
.
نعرِّف بوابة الفتل Twist بـ  التي تولِّد انزياحًا في طور الكيت بمقدار α.
التي تولِّد انزياحًا في طور الكيت بمقدار α.
وبوجه خاصّ نعرِّف البوابة-زي بـ Z = T(π) وبوابة-المُطابِق I = T(0)[2].
ونعرّف مصفوفة هادامارد Hadamard بـ  ، ومن ثَم فإن تطبيقها على أيّ حالة صرفة يعطي حالةً يمكن أن تكون في الحالة 0 أو 1 باحتمال 50/50، لأن:
، ومن ثَم فإن تطبيقها على أيّ حالة صرفة يعطي حالةً يمكن أن تكون في الحالة 0 أو 1 باحتمال 50/50، لأن:
 .
.
رابعًا) النُّظم المتعددة الكيوبتات Multi-qubit systems
بالتعميم، يمكن تمثيل حالة منظومة كمومية تتألف من n كيوبت قابلة للتمايز distinguishable بشعاع كيت ذي 2n مركّبة عقدية تدعى بالسعات amplitudes، حيث يمثل مربّع طويلة السعة ذات الرتبة 1 ≤ i ≤ 2n قيمةَ احتمال تداعي المنظومة إلى الحالة الصرفة ω الموافقة لتمثيل العدد (i-1) وفق النظام الثنائي على الـ n كيوبت: ω = (i-1)2، فنكتب (بعد مطابقة النشر وفق النظام الثنائي بطول n لـ (i-1) مع عنصرٍ في {0,1}n ):
 .
.
وكمثال على حالة منظومة ثنائية الكيوبت، لدينا:

حيث |aij|2 احتمال تداعي الكيوبت الأول (الثاني) إلى الحالة i (j) عند إجراء القياس.
خامسًا) النُّظم الفَصولة (القابلة للفصل) Separable
نعرِّف جداء كرونيكر Kronecker بين مصفوفة  ومصفوفة B دون شروط على أبعادها بالعلاقة:
ومصفوفة B دون شروط على أبعادها بالعلاقة:
![]()
 ،
،
وهذا جداء ثنائيّ الخطية وتجميعي ولكنه غير تبديلي عمومًا.
يحقِّق الجداءُ الخاصيةَ المهمّة التالية: عندما يكون الجداء المصفوفي Ai Bi مُعرَّفًا لكلّ i.
عندما يكون الجداء المصفوفي Ai Bi مُعرَّفًا لكلّ i.
نقول عن المنظومة في الحالة |ψ⟩ إنها فصولة separable إذا أمكن كتابتُها بصيغة جداء كرونيكر لحالات كيوبتاتها، أي  حيث الكيوبت ذي الرتبة i في الحالة |ψi⟩. يكافئ هذا الأمر قولَنا إن الكيوبتات تتداعى عند القياس بشكل مستقلّ بعضها عن بعض بالمعنى الاحتمالي.
حيث الكيوبت ذي الرتبة i في الحالة |ψi⟩. يكافئ هذا الأمر قولَنا إن الكيوبتات تتداعى عند القياس بشكل مستقلّ بعضها عن بعض بالمعنى الاحتمالي.
لتثبيت الأفكار، نأخذ الحالة n=2، و 
فيكون  ،
،
ومن ثَم يكون احتمال تداعي |ψ1 & |ψ2 ⟩ عند القياس إلى i & j يساوي |ai|2 . |bi|2 على الترتيب؛ أي يكون مساويًا جداء احتمال تداعي |ψ1⟩ إلى الحالة i باحتمال تداعي |ψ2⟩ إلى الحالة j ، وذلك أيًّا كانت الحالات i, j ∈ {0,1}.
يمكن إذن تمثيل منظومة كمومية فصولة بـ n كيوبت بشعاع عقدي في فضاء جزئي بعده 2n ضمن الفضاء المُحيط ذي الـ 2n بُعدًا.
إذا لم تكن منظومةُ الكيوبتات فصولةً قلنا إنها متشابكة entangled، ويُفترَضُ عادةً عند البدء بالحسابات الكمومية أن تكون جميع الكيوبتات فصولة، ولكن مع إجراء عمليّات خاصّة على أزواجٍ منها يمكنها أن تتشابك.
سادسًا) البوّابات والدارات circuits المتعددة الكيوبتات
البوابات الكمومية التي تؤثّر في منظومة ذات n كيوبت هي مصفوفات عقدية واحدية مربّعة أبعادها 2n. نقول عن بوابة كمومية إنها فصولة إذا أمكن كتابتُها بصيغة جداء كرونيكر لبوابات وحيدة الكيوبت، وتتميّز بأنها تُبقي الكيوبتات الفصولة غيرَ متشابكة. فمثلًا، تطبيق البوابة الفصولة U = X ⊗ H على الحالة الفصولة |ψ1⟩|ψ2⟩ يعطي حالةً فصولة  .
.
إن تمثيل البوابة U في الأساس B = (|00⟩, |01⟩, |10⟩, |11⟩) هو:

حيث يعطي العمود ذو الرتبة i مركّبات U = (Bi) وفق الأساس B.
مثال:  .
.
عند العمل على نظم ذات عدد كبير من الكيوبتات، يغدو التمثيل المصفوفاتي للبوابة معقّدًا بسبب التزايد الأسّي في عدد السطور والأعمدة. ولذلك نلجأ إلى الدارات الكمومية وهي مخطّطات تجعل من السهل التعامل مع العمليّات الكمومية. وكمثال توضيحي على ذلك، يمكن تمثيل البوابة في الشكل (2) بالعبارة:


الشكل (2): الدارة الممثلة لبوابة ثلاثية الكيوبتات 
إن أكثر البوّابات المُسبِّبة للتشابك هي بوابة النفي المُتحكَّم به CNOT المؤثِّرة في منظومة ثنائية الكيوبتات، ونرمز لها بالرمز:

ومن ثَم تنقل |x1⟩ |x2⟩ إلى |x1⟩ |x1 ⊕ x2⟩، أي تقلب (تُبقي) الكيوبت الثاني (كيوبت الهدف Target) شريطةَ أن يكون الكيوبت الأول (كيوبت التحكّم control) مساويًا الواحد (الصفر)، ومن ثَم فهي تُرمِّز عملية أو-الحصرية Exclusive OR بين كيوبِتَّي التحكّم والهدف ضمن كيوبت الهدف. يمثل الشكل (3) البوابة Λ1(X) حيث يُرمَّز كيوبت التحكّم بنقطة ثخينة.

الشكل (3): الدارة الممثّلة للبوابة CNOT
يمكن البرهان ([Kaye 2007]) على أن البوّابات H, T (π / 4), Λ1(X) شمولية universal، بمعنى إمكان تقريب أي بوابة كمومية باستعمال دارة كمومية لا تتضمّن إلّا هذه البوّابات[3].
سابعًا) التداخُل Interference وفكّ الترابُط Decoherence الكموميّان
يمكِّن ميكانيك الكمّ - بفضل ظاهرة التداخل الكمومي الناجمة عن مبدأ التراكُب الخطّي - من التحكّم بقيمة احتمال تداعي منظومة كيوبتات إلى حالات صرفة خاصّة منشودة. لنأخذ - للإيضاح - الكيوبت |ψ⟩ في حالة تراكُب خطي  ، فنجد أن H |ψ⟩ = 1⟩؛ وهذا يعني أننا إذا طبّقنا بوابة هادامارد على |ψ⟩ فإنها سوفَ تُرصَد عند القياس في الحالة الصرفة |1⟩ في بالتأكيد.
، فنجد أن H |ψ⟩ = 1⟩؛ وهذا يعني أننا إذا طبّقنا بوابة هادامارد على |ψ⟩ فإنها سوفَ تُرصَد عند القياس في الحالة الصرفة |1⟩ في بالتأكيد.
نلاحظ أن إمكان قياس |ψ⟩ في إحدى الحالتَين الكيوبت |0⟩ و|1⟩ بقيمتَي احتمال متساويتَين لا يعني أبدًا أن H |ψ⟩ = H |0⟩ باحتمال 50%، وأنH |ψ⟩ = H |1⟩ باحتمال 50%.
إضافة إلى ذلك، ولكي يتحقّق هذا الأمر ينبغي أن يقاس الكيوبت |ψ⟩ قبل تطبيق بوابة هادامارد. ونقول عن الكيوبت في هذه الحالة - بعد عملية قياسٍ غير مقصود - إنه في حالة مختلطة mixed[4]. يمكن كسر التداخل الكمومي إذن بإجراء عملية رصدٍ أو قياسٍ عَرَضيّ، وتُدعى هذه الظاهرة بفكّ الترابُط الكمومي، وهي مصدر لكثير من الأخطاء عند العمل مع حواسيب كمومية فيزيائية.
ثامنًا) الخوارزميّات الكمومية Quantum Algorithms – خوارزمية دويتش Deutsch
نشر دويتش عام 1985 ورقةً [Deutsch 1985] صاغ فيها نظرية التعقيد الكمومي Quantum Complexity Theory وآلات تورينغ الكمومية Quantum Turing Machines، ممّا سمح بمقارنة سرعة الحواسيب التقليدية إزاء الآلات الكمومية النظرية. وقد طرح دويتش في ورقته مسألةً وخوارزميةً كمومية لحلّها أشارت إلى إمكان زيادة سرعة الحسابات زيادة ملحوظة مقارنةً بخوارزميات تقليدية معروفة، وسنعرضها الآن كنموذج بدئي عن كيفية مقاربة الخوارزميات الكمومية.
المسألة: عيِّن فيما إذا كان التابع {0,1} → {0,1} ثابتًا بأقلّ عدد ممكن من حسابات قيم هذا التابع.
يستطيع الحاسوب التقليدي حلّ هذه المسألة بإجراء عمليّتَي حسابِ قيم، أي بحساب f(0) و f(1). بيّن دويتش أن حاسوبًا كموميًّا يمكنه من حيث المبدأ استخلاص قيمة f(0) ⊕ f(1) حالًا، مستفيدًا من التراكُب لحساب قيمتَي f(0) و f(1) معًا. حيث إنf(0) ⊕ f(1) تساوي الصفر إذا وفقط إذا كان f ثابتًا، ويمكننا القول إن الخوارزمية الكمومية تحتاج إلى عملية واحدة فقط في حسابِ قيمةِ f للإقرار بثباته أو عدم ثباته.
تعتمد الخوارزمية على البوابة الكمومية  التي وإن احتاج تعريفُها إلى تقدير قيمة التابع مرّتَين، فإن الخوارزمية تبيّن القدرة مبدئيًّا على معرفة ثبات التابع من عدم ثباته عن طريق تداول بِتّ واحد فقط. في الحقيقة يمكن التحقّق بسهولة من العلاقتَين:
التي وإن احتاج تعريفُها إلى تقدير قيمة التابع مرّتَين، فإن الخوارزمية تبيّن القدرة مبدئيًّا على معرفة ثبات التابع من عدم ثباته عن طريق تداول بِتّ واحد فقط. في الحقيقة يمكن التحقّق بسهولة من العلاقتَين:

واستنتاج العلاقة:

ومن ثَم - لغاية انزياحٍ في الطور - يغدو كيوبت التحكّم في حالةٍ متناسبة مع (1,1) في حال كون f ثابتًا، أو مع (1,-1) فيما عدا ذلك. وحيث إن هاتين الحالتَين تمثّلان أعمدة مصفوفة هادامارد نجد العلاقة النهائية الآتية:

وتتمثّل دارة الخوارزمية إذن في الشكل (4)، حيث يدلّ الكيوبت العلوي في الخرج على ثبات التابع أو عدم ثباته وفقًا لكونه في حالة 0 أو 1.

الشكل (4): الدارة الممثّلة لخوارزمية دويتش
تاسعًا) خلاصة وملاحظات أخيرة [Chamoun 2014]
قدّمنا عرضًا سريعًا لأساسيّات الحوسبة الكمومية، ولم نتعرّض إلى كيفية التحقيق الفيزيائي لها. تَستعمل الحوسبة الكمومية ظواهرَ ميكانيك الكمّ وخصوصًا التراكب الخطّي superposition للحالات والتشابُك entanglement لإنجاز عمليّات على المعطيات. تُسمَّى المنظومات التي تقوم بهذه العمليّات الحواسيب الكمومية Quantum Computers.
وعلى حين أن المعلومات تُخزَّن في الحاسوب الرقمي على شكل بتّات bits تكون في إحدى حالتَين (0 أو 1)، فإن الحاسب الكمومي يخزِّن المعلومات على شكل كيوبتات (أو بتّات كمومية) qubits هي تركيبات خطّية لبتّات.
لا تزال الحواسيب الكمومية في بداياتها وإن حصل بعض الحسابات الكمومية باستعمال عدد صغير جدًّا من البتات الكمومية. وستكون الحواسيب الكمومية حال إنجازها قادرةً على حلّ بعض المسائل - كمسألة تحليل الأعداد الصحيحة - بسرعة أكبر بكثير من سرعة الحواسيب التقليدية، وذلك باستعمال خوارزميّات كمومية quantum algorithms خاصّة، مثل خوارزمية شور Shor's algorithm التي توفر تسريعًا أسّيًّا في حالة تحليل الأعداد، ممّا يجعلها ذات كمونٍ جبّار في مجالات التعمية cryptography.
إن التعمية الكمومية quantum cryptography في الواقع أكثر أمانًا من التعمية التقليدية التي تعتمد أساسًا على رياضيّات نظرية الأعداد Number Theory، من حيث إنها تمكِّن شريكَين موصولَين بقناتَين تقليدية وكمومية غير آمنتَين (أي يمكن التنصّت eavedropping عليهما) من تبادل مفتاحٍ سرّيّ secret key بطريقة آمِنة بقطع النظر عن إمكانات المتنصِّت، وذلك لأن ميكانيك الكمّ يمنع الأخير من أن يقيس بنجاح الحالةَ الكموميةَ المنتقلةَ عبر القناة دون أن يتسبّبَ باضطرابٍ فيها يمكن كشفُه. ويعود سببُ ذلك إلى مبدأ التزاوُج الأحادي الكموميّ quantum monogamy الذي يمنع منظومتَين كموميّتَين متشابكتَين تشابكًا أعظميًّا من التشابُك مع منظومةٍ ثالثة.
وهكذا فإن التعمية الكمومية تنجز مهامَّ كان من المستحيل إنجازُها باستعمال قنوات اتّصال غير كمومية. وإلى جانب مجال التعمية، يمكن القول إن المعلومات الكمومية القائمة على أساس البتات الكمومية تختلف جذريًّا عن المعلومات التقليدية القائمة على أساس البتات. وثمة نظريّات عديدة تعالِج العلاقات بين نوعَي المعلومات، كنظرية عدم النقل عن بعد no-teleportation التي تنصّ على عدم إمكان تحويل البتات الكمومية إلى مجرّد بِتّات قابلة للقراءة بدقّة لامتناهية (مع ملاحظة إمكان نقل المعلومات الكمومية عبر قناة تقليدية مع وجود تشابُك كمومي سابِق بين المُرسِل والمستقبِل ضمن إجرائية النقل الكمومي عن بعد quantum teleportation)، ونظرية عدم الاستنساخ الكمومي no cloning عن عدم إمكان نسخ البتات الكمومية أو تدميرها، وغيرها.
المراجع:
- R. P. Feynman. Simulating physics with computers. International Journal of Theoretical Physics, 21(6): 467–488, 1982. .
- Deutsch. Quantum theory, the Church-Turing principle and the universal quantum computer. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 400(1818): 97–117, 1985.
- L. K. Grover. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing, pages 212–219. ACM, 1996.
- P. W. Shor. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Journal on Computing, 26(5): 1484–26, 10 1997.
- IBM Quantum Experience.
https://quantumexperience.ng.bluemix.net/qstage/#/user-guide
- P. Kaye, R. Laflamme, and M. Mosca. An Introduction to Quantum Computing. Oxford University Press, 2007.
- نضال شمعون Chamoun، التشابك الكمومي، الموسوعة العربية 2014.
[1] تعني ضرورةُ تنظيم الكيت على أنه شعاع واحدة في فضاء هلبرت إذن مجرَّدَ وجودِ تفسيرٍ احتماليّ لمعاملات التركيب الخطّي.
[2] تتناسب المصفوفتان Z,X مع مصفوفتَي باولي σz, σx المولّدتَين للدورانَين حول المحورَين z, x في ميكانيك الكمّ.
[3] لا حاجة لتعريف النظيم المُستعمَل في التقريب صراحة، وذلك بسبب أن جميع أشكال النظيم في فضاء منتهي الأبعاد متكافئة.
[4] يُعبَّر عن الحالة المختلطة بـمصفوفة الكثافة density matrix  حيث 0<ps و
حيث 0<ps و وتدلّ على توزيعٍ احتمالي probability distribution للمنظومة التي هي في قيد الدراسة، أو على مجموعة إحصائية Ensemble لنُظُم متطابقة موجودة بنسبة ps في الحالة |ψ⟩ (ومن ثَم يمكنها كذلك توصيف الحالة الكمومية الصرفة |ψs0⟩ حيث تكون ps0 = 1).
وتدلّ على توزيعٍ احتمالي probability distribution للمنظومة التي هي في قيد الدراسة، أو على مجموعة إحصائية Ensemble لنُظُم متطابقة موجودة بنسبة ps في الحالة |ψ⟩ (ومن ثَم يمكنها كذلك توصيف الحالة الكمومية الصرفة |ψs0⟩ حيث تكون ps0 = 1).









 ما هي الحوسبة الكمومية
ما هي الحوسبة الكمومية التعمية بعد الكمومية
التعمية بعد الكمومية التعمية الكمومية
التعمية الكمومية نظم حوسبة كمومية قائمة
نظم حوسبة كمومية قائمة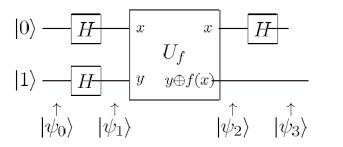 خوارزميات كمومية
خوارزميات كمومية