بعد أن أعلنت منظمة الصحة العالمية كورونا وباءً عالميًّا، صار من المهم جدًّا تضافر الجهود حول العالم لكبح هذا المرض الخطر، لاسيما وأن اكتشاف لقاح فعال له لا يزال أمرًا يتطلب المزيد من الوقت. لذلك لا بد أن ینصبَّ التركيز على إبطاء انتشاره.

ولما كانت التقانات الحديثة مصمَّمة لخدمة البشر، فقد أصبح توظيفها في الصراع الدائر ضد هذا الفيروس أمرًا بالغ الأهمية. وقد حققت الصين مؤخرًا تطورًا لافتًا بكبح جماح انتشار المرض معتمدة على التقانات الحاسوبية، ومن أهمها الذكاء الصناعي والروبوت.

يَعرض هذا المقال تقنية في النمذجة الرياضية للتنبؤ بانتشار الوباء، وهو نموذج S-I-R، وذلك بتحويل المتغيرات المتعلقة بالوباء إلى لغة رقمية بمساعدة معدلات التغير مع الزمن لأجزاء معيَّنة في العيِّنة السكانية المدروسة، تمتلك كلٌّ منها خصائص متشابهة في هذا النموذج، ثم تصميم نموذج حاسوبي على أداة SIMULINK في MATLAB لتنفيذ عملية المحاكاة، التي أعطت تقديرات مهمة عمَّا يمكن فعله للحد من انتشار الوباء.

 

مقدمة عن فيروس كورونا

ينتمي فيروس كورونا إلى فصیلة كبیرة من الفيروسات التي تسبب المرض للإنسان والحيوان؛ إذ إن عددًا من فیروسات كورونا تسبب عدوى الجھاز التنفسي التي تراوح شدتها من حالات نزلات البرد المعروفة إلى الأمراض التي هي أشدّ سوءًا؛ مثل متلازمة الشرق الأوسط التنفسیة والمتلازمة التنفسیة الحادة (سارس).

وأهم الأعراض الناتجة عن فیروس كورونا المُكتشف حديثًا الحمى والإرھاق والسعال الجاف. وقد یعاني بعض المرضى من الآلام والأوجاع، أو احتقان الأنف، أو الرشح، أو ألم الحلق، أو الإسھال. وعادة ما تكون ھذه الأعراض خفیفة ثم تتفاقم تدریجیًّا. ویصاب بعض الناس بالعدوى دون أن تظھر علیھم أي أعراض ودون أن یشعروا بالمرض. ویتعافى معظم الأشخاص (نحو 80% من المرضى دون الحاجة إلى علاج خاص). وتشتد حدة المرض لدى شخص واحد تقریبًا من كل 6 أشخاص یصابون بالمرض حیث یعانون من صعوبة في التنفس. وتزداد احتمالات إصابة المسنین والأشخاص الذين لديهم مشكلات طبیة أساسیة مثل ارتفاع ضغط الدم أو أمراض القلب أو داء السكري بأعراض سيئة. ولذلك، فإن على الذین یعانون من الحمى والسعال وصعوبة في التنفس أن يطلبوا الرعایة الطبیة.

یمكن أن یصاب الأشخاص بالعدوى عن طریق المصابین بالفیروس. ویمكن أن ینتقل المرض من شخص إلى آخر عن طریق القُطیرات الصغیرة التي تتناثر من الأنف أو الفم عندما یسعل المصاب أو یعطس. وتتساقط ھذه القُطیرات على الأشیاء والأسطح المحیطة بالشخص. ویمكن حینھا أن یصاب الأشخاص عند ملامستھم لھذه الأشیاء أو الأسطح ثم لمس العين أو الأنف أو الفم. ویمكن أن یصاب الأشخاص إذا تنفسوا القُطیرات التي تخرج من الشخص المصاب بالمرض مع سعاله أو زفیره.

 

النمذجة الرياضية للأوبئة

النمذجة الرياضية هي تحويل المشكلة الواقعية إلى صياغة رياضية بواسطة سلسلة عمليات منهجية يوضحها الشكل 1، حيث يجري التعامل مع المشكلة رياضيًّا، ليتم بعد ذلك إسقاط النتائج على أرض الواقع لحل المشكلة المطروحة.

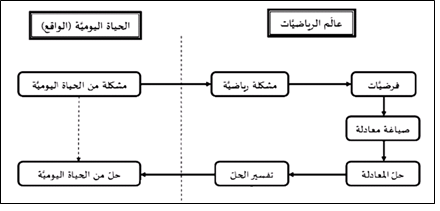
الشكل 1: خطوات النمذجة الرياضية

 

في النمذجة الرياضية للأوبئة تقسَّم العيِّنة السكانية المدروسة إلى عدة أجزاء مع افتراض أن الأشخاص في كل جزء من هذه الأجزاء متشابهون في الخصائص.

كانت أولى المحاولات لتصميم النماذج الرياضية للأوبئة على يد كلٍّ من Kermack و McKendrick عام 1927.

تستند أغلب النماذج الرياضية للأوبئة إلى المعادلات التفاضلية العادية، وهي نظم قطعية (حتمية)، لكن من الممكن إدخال عنصر الاحتمالية إلى تلك النماذج وجعلها نظمًا احتمالية، وهي أكثر واقعية من النظم القطعية، ولكنها أشد تعقيدًا وأقل مرونة في التحليل والتنبؤ.

تُستعمل نماذج الأوبئة في التنبؤ بكيفية انتشار الوباء، مثل عدد الأشخاص المصابين ومدة الوباء. وهي تتيح فهم الحالات المختلفة التي تؤثر في الوباء والإجراءات الأشد فعالية للحد من انتشاره.

 

نموذج S-I-R

هناك نماذج رياضية عديدة لنمذجة انتشار الأوبئة، أحد أشد هذه النماذج أهمية وبساطة في نفس الوقت: نموذج S-I-R، وهذه الأحرف هي الأحرف الأوائلية للكلمات الثلاث:

Susceptible- Infectious- Recovered

أي: المعرَّض للإصابة-المصاب-المتعافى (أي كان مريضًا ثم تعافى)، على الترتيب

حيث:

I : عدد المصابين خلال مدة معيَّنة.

S: عدد المعرضين للإصابة خلال المدة نفسها.

R: عدد المتعافين خلال المدة نفسها (أي كانوا مرضى ثم تعافوا).

وهنا لا بد من تعريف متغيرَين أساسيين أيضًا هما:

  m[1/time]: معدل تحول المعرضين للإصابة إلى مصابين خلال المدة نفسها.

r [1/time]: معدل تحول المصابين إلى متعافين خلال المدة نفسها.

التفاعل بين هذه المكونات الثلاثة موضح في الشكل 2.

 

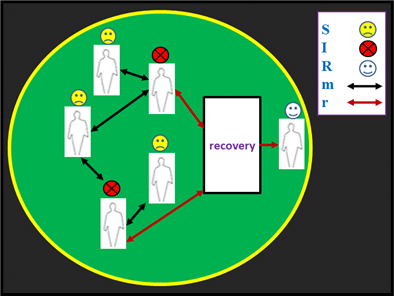
الشكل 2: تمثيل توضيحي للتفاعل بين مكونات نموذج S-I-R

 

واستنادًا إلى ما سبق يمكن وضع المعادلات التفاضلية الثلاث التالية المعبرة عن معدلات تغير عدد المعرضين للإصابة والمصابين والمتعافين على الترتيب:

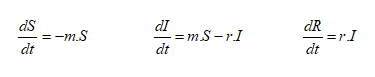
حيث:

[individual/time] dS/dt: التغير في عدد المعرضين للإصابة خلال مدة معيَّنة.

[individual/time] dI/dt: التغير في عدد المصابين خلال المدة نفسها.

[individual/time] dR/dt: التغير في عدد المتعافين خلال المدة نفسها.

إن معدل تحول المعرضين للإصابة إلى مصابين خلال مدة معيَّنة يتوقف على:

1.  [1/time] a احتمال اتصال الأشخاص في بؤرة المرض بعضهم ببعض في مدة معيَّنة (النسبة المئوية لمتوسط الوقت الذي يقضيه الشخص وهو في حالة اتصال بالآخرين خلال مدة معيَّنة).
2. I/N احتمال أن يكون الاتصال بأشخاص مصابين (نسبة عدد المصابين إلى العدد الإجمالي للعيِّنة السكانية في بؤرة المرض N) حيث: N = S + I + R  أي العدد الإجمالي لكلٍّ من المعرضين للإصابة والمصابين والمتعافين.
3. b احتمال انتقال المرض عند اتصال مريض بشخص آخر (النسبة المئوية لحالات الإصابة من كل مئة حالة اتصال بين مريض وغير مريض).

أما معدل تحول المصابين إلى متعافين r، فيساوي مقلوب مدة المرض D، أي إذا كانت مدة المرض للشخص الواحد تبلغ في المتوسط 10 أيام مثلًا، فهذا يعني أنه يتماثل للشفاء بمعدل 0.1 يوميًّا.

وهكذا يصبح نموذج S-I-R رياضيًّا كما يلي:

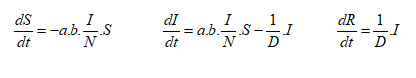
وهي جملة مؤلفة من ثلاث معادلات تفاضلية عادية لاخطية، وليس لها حلٌّ تحليليٌّ أبدًا، ولكن يمكن حلُّها بالطرق العددية باستعمال الأداة SIMULINK كما هو مبين في الشكل 3، وهي أداة محاكاة حاسوبية متقدمة ضمن برمجية MATLAB. تستطيع هذه الأداة تحويل أي ظاهرة مدروسة إلى لغة مخططات صندوقية اعتمادًا على النموذج الرياضي لتلك الظاهرة.

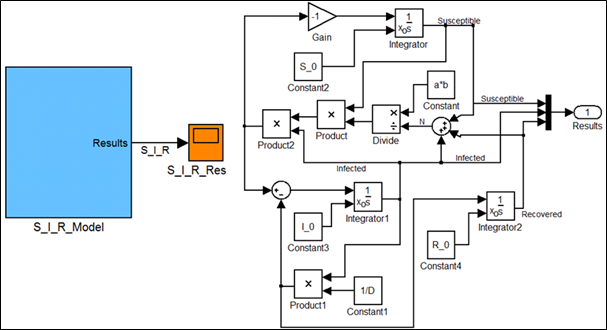
الشكل 3: مخطط صندوقي باستعمال SIMULINK لنموذج S-I-R

 

نتائج المحاكاة

لتبسيط النتائج وعرضها عرضًا قابلًا للتفسير، نطبِّق المحاكاة على عيِّنة سكانية مكونة من 700 شخص تمثل بؤرة المرض المكتشف، ونفترض القيم الآتية:

العدد الأولي للمتعافين R_0=0 (حيث بدأت المحاكاة عند أول حالة إصابة مكتشفة: I_0=1، بمعنى أنه لم يتماثل أحدٌ للشفاء بعدُ).

 a=0.3 احتمال البقاء خارج المنزل يوميًّا (أي متوسط عدد ساعات الخروج يوميًّا إلى إجمالي عدد ساعات اليوم).

b=0.8 احتمال بقاء فيروس كورونا حيًّا في الهواء مدة 45 دقيقة تقريبًا بعد حالة سعال أو عطاس لمريض، وانتشاره على بعد 4 أمتار تقريبًا من المريض. وهذا يعني أن معدل الإصابة مرتفع وخطر.

D=10 أي إن مدة المرض تستمر نحو 10 أيام  (وهي فقط قيمة افتراضية ماتزال الاستقصاءات الطبية تتحرى دقتها).

 

يمثل المحورُ الأفقي الزمنَ بالأيام، ويمثل المحورُ العمودي عددَ الأشخاص.

• تأثير العدد الأولي للمعرضين للإصابة في بؤرة المرض

أُجريت المحاكاة بافتراض عيِّنة سكانية مؤلفة من 700 شخص، فيها شخص واحد مصاب.

وعيِّنة سكانية مؤلفة من 500 شخص فيها شخص واحد مصاب.

يُظهر الشكل 4 نتائج المحاكاة في الحالتين.

المنحنيات الحمراء تمثِّل تغير عدد المعرضين للإصابة

المنحنيات الزرقاء تمثِّل تغير عدد المصابين

المنحنيات السوداء تمثِّل تغير عدد المتعافين

المنحنيات المستمرة تمثِّل الحالة الأولى

المنحنيات المنقطة تمثِّل الحالة الثانية

من الواضح أن عدد المصابين الأعظمي انخفض من 150 تقريبًا في الحالة الأولى إلى أكثر من 100 بقليل في الحالة الثانية. هنا لا تُظهر المحاكاة أثرًا كبيرًا في سرعة انتشار المرض، بمعنى أن مدة انحدار المنحني ذي اللون الأحمر بقيت تقريبًا نفسها في الحالتين.

 

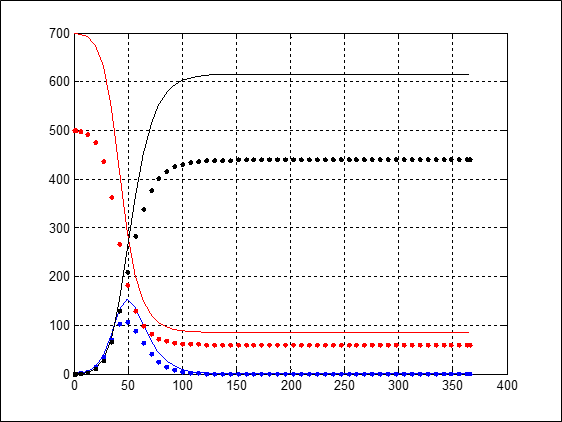
الشكل 4: تأثير العدد الأولي للمعرضين للإصابة في نموذج S-I-R

 

• تأثير الاتصال اليومي بين الأشخاص في بؤرة المرض

أُجريت المحاكاة بافتراض عيِّنة سكانية مؤلفة من 700 شخص فيها شخص واحد مصاب في الحالتين، لكن a=0.3 في الحالة الأولى، و a=0.2 في الحالة الثانية، أي إن معدل الخروج اليومي للأشخاص في الحالة الأولى 8 ساعات تقريبًا، انخفض إلى أقل من 5 ساعات في الحالة الثانية.

يُظهر الشكل 5 نتائج المحاكاة في الحالتين.

من الواضح أن عدد المصابين الأعظمي انخفض من 150 تقريبًا في الحالة الأولى إلى 60 تقريبًا في الحالة الثانية.

وتباطأ انتشار المرض بدرجة كبيرة (اتساع مدة انحدار المنحني ذي اللون الأحمر في الحالة الثانية).

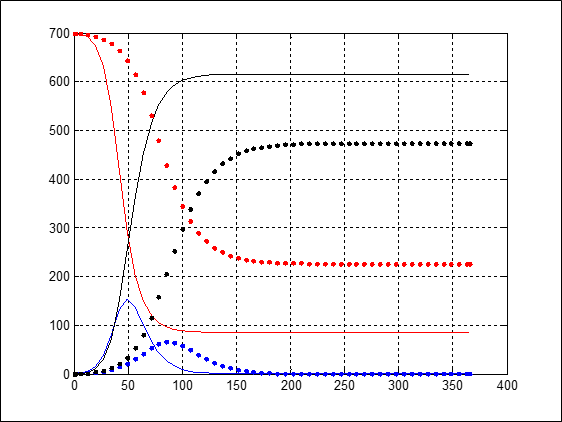
الشكل 5: تأثير معدل الاتصال اليومي بين الأشخاص في بؤرة المرض في نموذج S-I-R

 

• تأثير احتمال انتقال العدوى في بؤرة المرض

أُجريت المحاكاة بافتراض عيِّنة سكانية مؤلفة من 700 شخص فيها شخص واحد مصاب في الحالتين، لكن b=0.8 في الحالة الأولى، و b=0.6 في الحالة الثانية، وهذا يعني أنه حصل تطور طبي أو إجراء احترازي فعال خفَّض احتمال الإصابة من كل مئة حالة اتصال بين مريض وغير مريض من 80 حالة إصابة إلى 60 حالة إصابة.

يُظهر الشكل 6 نتائج المحاكاة في الحالتين.

من الواضح أن عدد المصابين الأعظمي انخفض من 150 تقريبًا إلى أقل من 100.

وتباطأ انتشار المرض تباطؤًا ملحوظًا (اتساع مدة انحدار المنحني ذي اللون الأحمر في الحالة الثانية).

 

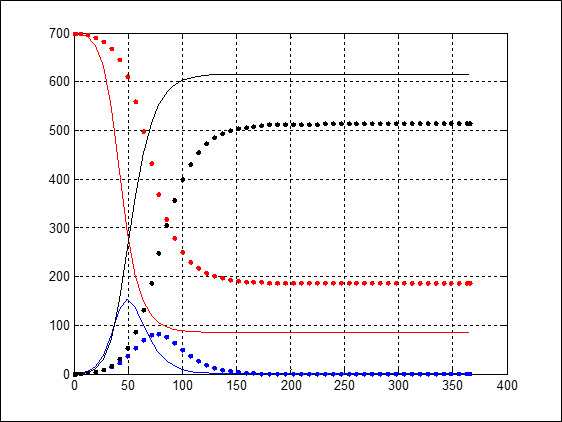
الشكل 6: تأثير سرعة العدوى بالمرض في نموذج S-I-R

 

• تأثير مدة المرض في بؤرة المرض

أُجريت المحاكاة بافتراض عيِّنة سكانية مؤلفة من 700 شخص، فيها شخص واحد مصاب في الحالتين، لكن D=10 في الحالة الأولى، و D=7 في الحالة الثانية. وهذا يعني أن هناك إنجازًا طبيًّا سواء على صعيد اكتشاف دواء أو لقاح أو رعاية طبية عاجلة وفعالة أدى إلى جعل مدة الإصابة بالمرض تنخفض من 10 أيام إلى 7 أيام.

يُظهر الشكل 7 نتائج المحاكاة في الحالتين.

من الواضح أن عدد المصابين الأعظمي انخفض من 150 تقريبًا إلى 60 تقريبًا.

وكذلك تباطأ انتشار المرض تباطؤًا واضحًا (اتساع مدة انحدار المنحني ذي اللون الأحمر في الحالة الثانية).

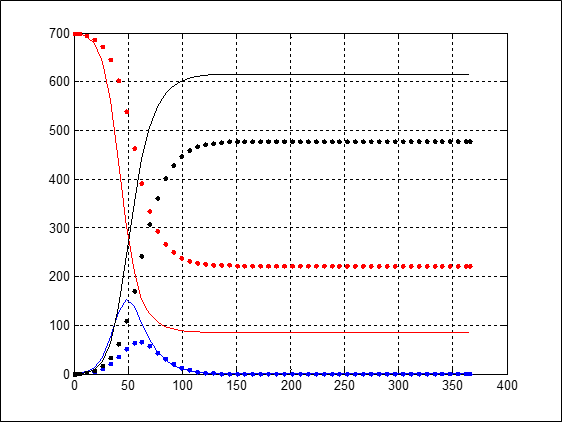
الشكل 7: تأثير مدة المرض في نموذج S-I-R

 

• تأثير تخفيض متزامن لقيم a و b و D

إذا افترضنا حالة جرى فيها اتخاذ جملة إجراءات متزامنة عاجلة وفعالة بحيث تكون: a=0.2  b=0.7   D=8، ثم طُبقت المحاكاة للمقارنة بالحالة الأصلية المفترضة، كما في الشكل 8، فإن المحاكاة تُظهر انتشارًا بطيئًا جدًّا للمرض (اتساع كبير في مدة انحدار المنحني ذي اللون الأحمر في الحالة الثانية)، وأن عدد المصابين قليل جدًّا مقارنة بكل الحالات السابقة (ارتفاع طفيف في المنحني ذي اللون الأزرق في الحالة الثانية).

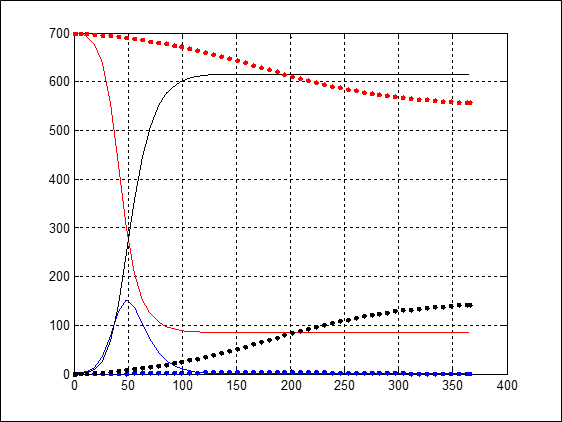
الشكل 8: تأثير اتخاذ جملة إجراءات متزامنة (تخفيض قيم D b a) في نموذج S-I-R

 

الاستنتاجات

          1. من نتائج المحاكاة السابقة يمكن أن نستنتج العوامل المتغيرة في النموذج الرياضي والتي يمكن ضبطها للسيطرة على انتشار الوباء وهي:

S: عدد المعرضين للإصابة خلال مدة معيَّنة.

يمكن تقليل هذا العدد بمنع السفر من بؤرة المرض وإليها (إغلاق بؤرة المرض).

a: احتمال اتصال الأشخاص في بؤرة المرض بعضهم ببعض (النسبة المئوية لمتوسط الوقت الذي يقضيه الشخص وهو في حالة اتصال بالآخرين خلال المدة نفسها).

يمكن تقليل هذا العدد بالحد من تحركات الناس في بؤرة المرض لمنع الاحتكاك بالمصابين (حالة الطوارئ في بؤرة المرض).

b: احتمال انتقال المرض عند اتصال مريض بشخص آخر (النسبة المئوية لحالات الإصابة من كل مئة حالة
اتصال بين مريض وغير مريض).

يمكن تقليل هذا العدد باتخاذ إجراءات وقائية ضرورية مثل الكمامات (الفرق الطبية في بؤرة المرض)، إضافة إلى إجراءات العزل.

r: معدل تحول المصابين إلى متعافين، وهو يساوي مقلوب مدة المرض D.

يمكن زيادة هذا المعدل بتقليل مدة المرض، وذلك ببناء مستشفيات بأقصى سرعة ممكنة خاصة بعلاج المرضى وإخضاعهم لعلاجات فعالة، وسيكون للكشف عن دواء أو لقاح فعال ضد المرض أثر حاسم في زيادة هذا المعدل حتمًا.

          2. إن اتخاذ سلسلة إجراءات متزامنة تؤدي إلى تخفيض قيم a b D معًا يعطي فعالية كبيرة في كبح انتشار المرض.

         3. من الممكن تطبيق النموذج على عينات سكانية اشتُبه بوجود المرض فيها، وبقدر ما تكون مدخلات النموذج صحيحة وواقعية تكون المخرجات صحيحة وواقعية، وهذا يحتم إعداد خطة وطنية شاملة طبية وخدمية واستقصائية.

         4. تُساعد المحاكاةُ والخوارزمياتُ العدديةُ النموذجَ على اتخاذ القرار الأمثل في الحالات الطارئة؛ من قبيل: ما هو معدل الخروج اليومي المسموح به للسكان لجعل انتشار المرض يتباطأ بمقدار 30% في الحالات التي تبيَّن فيها مثلًا أن معدل المصابين بالمرض فعليًّا أكبر من الأرقام المكتشَفة؟

 

التوصيات

يمكن الاستفادة من النمذجة الرياضية والمحاكاة الحاسوبية في التنبؤ بانتشار المرض، والتي أوضحت تأثير مختلف المتغيرات على سرعة انتشار المرض وساعدت مبدئيًّا على وضع التوصيات الآتية:

1. إغلاق بؤرة المرض.
2. إعلان حالة الطوارئ في بؤرة المرض، وهذه نقطة بالغة الأهمية لتأثيرها المباشر على كل الموسطات parameters التي تفاقم انتشار المرض؛ فقد بيَّنت المحاكاة أن الحد من تحركات الناس في بؤرة المرض يؤثر في جميع المتغيرات الهامة، وعلى وجه التحديد a و b.
3. تسيير الدوريات الطبية لتنفيذ الحجز الصحي على كل من يُشتبه بإصابته بالفيروس.
4. ضرورة استعمال الكمامات والتقيد بقواعد النظافة والتعقيم ومختلف الإجراءات الوقائية للحد من الإصابة ومن سرعة انتشار المرض.
5. الالتزام بالقوانين والتعليمات الصادرة عن الجهات المسؤولة لمواجهة أي تطور قد يحصل، وهذه نقطة هامة جدًّا حيث إن تعاون الناس مع السلطات في حالات حساسة كهذه سيكون له تأثير كبير في اتخاذ القرارات المناسبة للحد من انتشار المرض.
6. الإسراع في بناء المستشفيات والمراكز الصحية التي تعتني بمرضى هذا الفيروس، وتكثيف الأبحاث لإيجاد العلاج المناسب واللقاح الواقي من المرض.
7. يمكن بالاستفادة من المحاكاة تحليل البيانات لتحديد القرارات الواجب والممكن اتخاذها؛ فمثلًا إذا كان السؤال: أيهما أشد فعالية إعلان الطوارئ أم بناء المستشفيات؟ فإن الجواب يتوقف على المتاح فعلًا لدى السلطات من خطط وموارد وسرعة استجابتها للتطورات، حيث يمكن تنفيذ المحاكاة لمعرفة ما هو الرقم الممكن الوصول إليه لكل من a و D الذي يمثل كلٌّ منهما على التوالي الصيغة الرقمية للقرارين السابقين ليجري بعدها اتخاذ القرارات المثلى، وهذا ينطبق على جميع المتغيرات في النموذج والمحددة لمختلف القرارات الممكن اتخاذها.
8. توظيف التقانات المتقدمة المختلفة للحد من انتشار المرض تأسِّيًا بالصين، كاستعمال الذكاء الصنعي في تطبيقات موبايل مخصصة لمتابعة حالة المرضى والإبلاغ عن المشتبه بإصابتهم، وكذلك تقانات الروبوت لتخديم المرضى والاعتناء بهم.
9. لدى الجمعية العلمية السورية للمعلوماتية في اللاذقية ثلاثة أندية علمية هي: النمذجة والمحاكاة، والروبوت، والذكاء الصنعي، وهي مستعدة لتوظيف التقنيات التي تهتم بها للمساعدة على مواجهة أي غزو محتمل لهذا الفيروس.

المراجع:

"A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action"
Qianying Lina , Shi Zhaob, Daozhou Gaod , Yijun Loue , Shu Yangf , Salihu S. Musae , Maggie H. Wangb,c , Yongli Caig  Weiming Wangg, Lin Yangh, Daihai Hee, International Journal of Infectious Diseases-2020

"Mathematical Modeling of Infectious Diseases Dynamics"
M. Choisy,  J.-F. Guégan, and P. Rohani, Encyclopedia of Infectious Diseases: Modern Methodologies, by M.Tibayrenc
John Wiley & Sons, Inc.-2007

"The Mathematical Modeling of Epidemics"
Mimmo Iannelli, Mathematics Department University of Trento-Italy-2005